El modelo de Rutherford de 1911 tenía dos grandes limitaciones:
El átomo de Rutherford era inestable.
En el contexto de la teoría ondulatoria de la luz, la teoría electromagnética de Maxwell predecía que el electrón, al sufrir una aceleración normal, debería emitir continuamente energía en forma de ondas electromagnéticas. Esta pérdida continua de energía provocaría que el electrón terminaría describiendo órbitas de menor radio, en espiral, hasta chocar con el núcleo. Este fenómeno se conocía como colapso atómico.
Los espectros de emisión debían ser continuos.
La emisión de energía era continua y gradual, por lo que se esperaba la observación de un espectro de emisión continuo.

Esto no sucedía, pues los espectros de emisión de los átomos son discontinuos.

En 1913, el físico Niels Bohr propuso un modelo para el átomo que buscaba explicar la estabilidad de las órbitas de los electrones alrededor del núcleo y que interpretaba el espectro discontinuo del átomo. Para ello, aplicaba la hipótesis de Planck sobre la cuantización de la energía. El modelo de Bohr fue el primero que incluyó ideas cuánticas, además de las clásicas, y se desarrolló a partir de tres postulados.
Momento angular del electrón
L es una magnitud vectorial:

Como las órbitas de Bohr son circulares, el ángulo que forman r y v es de 90°, por lo que el módulo del momento angular es:
L = r ⋅m⋅ v ⋅sen 90 = r ⋅m⋅ v

4.1. Primer postulado de Bohr y cálculo de la velocidad
Para superar el problema de la inestabilidad del átomo, Bohr supuso que los electrones solamente podían describir órbitas específicas, caracterizadas por su nivel energético, denominadas órbitas estacionarias. Cada una de ellas puede identificarse mediante un número entero n.
Bohr postuló que el electrón no debía emitir energía mientras se mantuviera en una de estas órbitas, contradiciendo las predicciones de las teorías clásicas del electromagnetismo, formuladas en el contexto de la teoría ondulatoria.
El primer postulado de Bohr indica que los electrones giran alrededor del núcleo en órbitas circulares, denominadas órbitas estacionarias, sin emitir energía.
Para mantenerse en órbita, manteniendo el equilibrio mecánico, la fuerza de atracción eléctrica del electrón por el núcleo debe actuar como una fuerza centrípeta. De manera que, igualando los módulos de las fuerzas, obtenemos:
Despejando la expresión de la velocidad al cuadrado del 1.er postulado, obtenemos:

subtitulo
- Observa la dependencia de la velocidad orbital con el radio y contesta:
- Cómo varía la velocidad orbital en un átomo?
- ¿Están cuantizados los valores de los radios orbitales en el átomo de Bohr?
- Justifica si cada órbita tendrá una energía cuantificada.
4.2. Segundo postulado de Bohr y cálculo del radio de la órbita
Además de que el electrón giraba en órbitas estacionarias sin emitir energía, Bohr supuso que estas órbitas permitidas estaban caracterizadas por el momento angular de cada electrón, que estaba cuantizado y solo podía variar en fracciones enteras de la constante de Planck.
El segundo postulado de Bohr plantea que las órbitas permitidas al electrón son aquellas en las que su momento angular está cuantizado y su valor es un múltiplo entero de  .
.
 , donde n = 1, 2, 3
, donde n = 1, 2, 3
Bohr calculó para cada nivel energético, n, la distancia a la cual se hallaba del núcleo, es decir, el radio de cada una de las órbitas permitidas en el átomo:
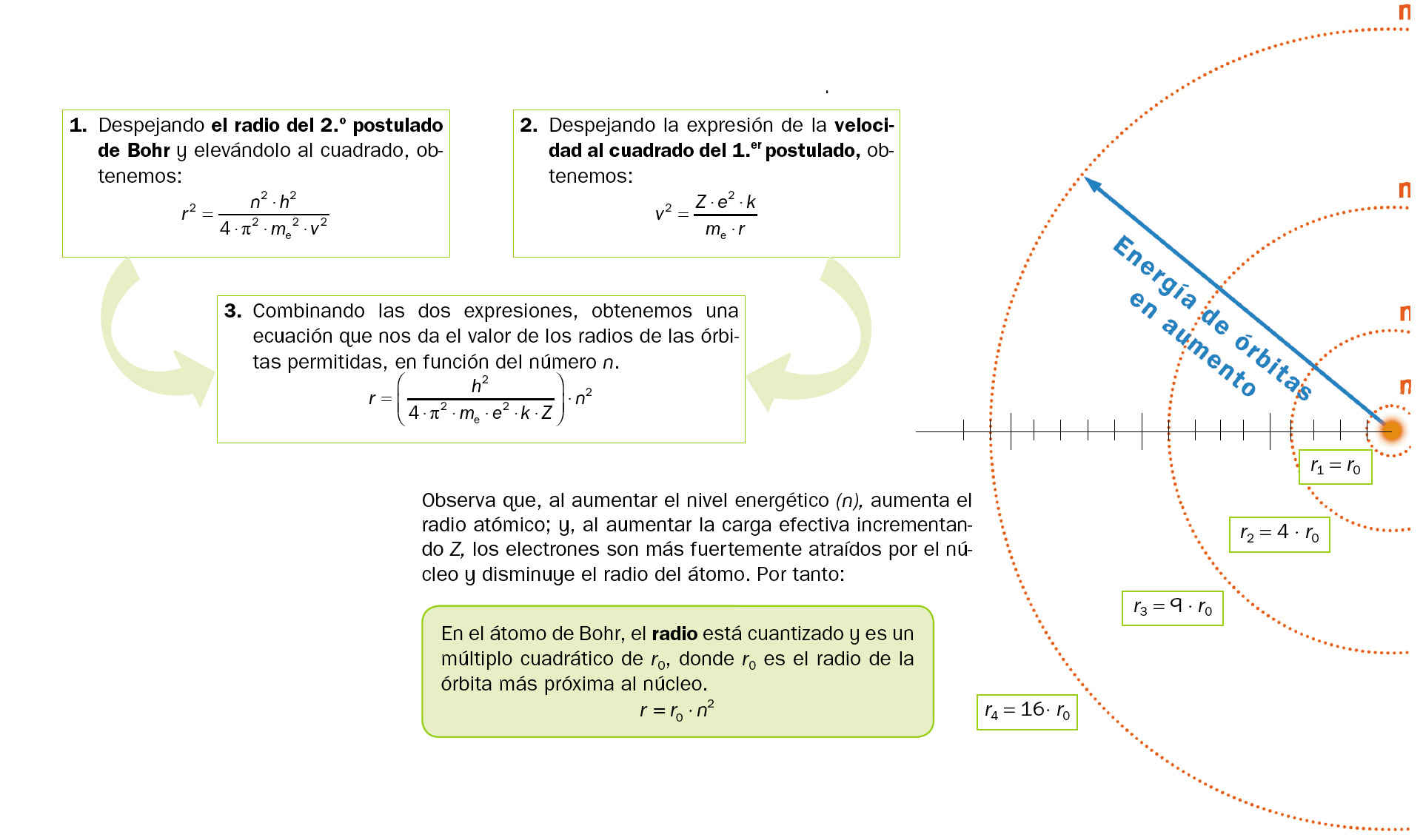
Para el átomo de hidrógeno, r0 (Z = 1) = 0,53 Å y se denomina radio de Bohr.
subtitulo
- Justifica si las siguientes afirmaciones sobre el átomo de Bohr son ciertas:
- Los electrones tienen aceleración, a pesar de no variar su energía.
- Los electrones no tienen aceleración por estar en órbitas estables.
- Los electrones tienen la misma velocidad en cualquier órbita.
- Los electrones pueden adoptar cualquier valor de la energía.
- Sabiendo que el radio de Bohr r0 = 0,53 Å, determina el radio del átomo de hidrógeno, helio y litio, y compara los resultados con los valores reales 53 pm, 31 pm y 167 pm, respectivamente.
S: r(H) = 53 pm; r(He) = 26,5 pm; r(Li) = 106 pm
4.3. Tercer postulado y cálculo de la energía del electrón
Con su tercer postulado, Bohr propuso que los electrones excitados eran los responsables de los saltos electrónicos y, por tanto, de la aparición de las rayas en los espectros.
El tercer postulado de Bohr indica que, cuando un electrón pasa de una órbita a otra, absorbe o emite radiación electromagnética cuya energía es la diferencia entre las energías de la órbita final e inicial.
E = Ef − Ei = h⋅ν

subtitulo
- Determina las energías de los cinco primeros niveles energéticos del átomo de Bohr.
- Para las siguientes energías, establece si son posibles y a qué nivel del átomo de hidrógeno corresponden. ¿Y si fuera el átomo de helio (Z = 2)?
a) 3,400 eV b) −1,305 eV c) −6,044 eV d) −0,850 eV e) −2,176 eV f) −2,550 eV
4.4. El espectro del hidrógeno
Bohr interpretó el espectro de emisión del hidrógeno relacionando las líneas observadas con las transiciones de los electrones desde niveles más energéticos a otros de menos energía con la consecuente emisión de energía. Se descubrieron cinco series de líneas, que toman el nombre de sus descubridores.
La energía desprendida o absorbida por un electrón al pasar de una órbita n0 a una órbita nf se determina mediante el tercer postulado de Bohr:

Observa cómo necesitarás una constante diferente según uses una fórmula u otra.

Si nf > n0,
ΔE > 0, energía absorbida.
Si nf < n0.
ΔE < 0 energía emitida.
Esta última fórmula fue descubierta ya en 1890 por el físico sueco Rydberg, quien observó que las longitudes de ondas de las líneas obedecían a esa ecuación empírica. Rydberg dio, además, nombre a la constante RH.
subtitulo
Determina para el átomo de hidrógeno la energía necesaria para ionizar un átomo que se encuentra en el estado fundamental. ¿Y si el electrón está en el nivel n = 2?
Para ionizar el átomo, debemos arrancar el electrón, es decir, llevarlo desde el nivel que se encuentre hasta la órbita más alejada, fuera de la influencia del núcleo donde tomamos n = ∞ y la energía es E∞= 0.
|
1. En el estado fundamental está el primer nivel. Su energía es E1 = −13,6 eV.
ΔE = E∞ − E1
ΔE = (0 eV) − (−13,6 eV) = 13,6 eV
|
2. Si inicialmente está el segundo nivel,
su energía será E2 = −3,4 eV.
ΔE = E∞ − E2
ΔE = (0 eV) − (−3,4eV) = 3,4 eV
|
subtitulo
- Obtén las energías del espectro de emisión que finaliza en el tercer nivel en función de E0. Particularízalo para el átomo de hidrógeno y para el helio catión +1. Considera hasta el sexto nivel. Por último, elabora una hoja de cálculo que permita obtener estos valores para cualquier nivel inicial, consuta los datos: bit.ly/2BAC_U1_Espectros_niveles
S: 
