Els nombres enters són el conjunt format pels nombres naturals, el zero i els nombres negatius (−1, −2, −3...). Es representen amb el símbol ℤ:
La recta numèrica també es pot representar en vertical, com l'escala graduada que hi ha en un termòmetre o l'esquema dels pisos que té un edifici.
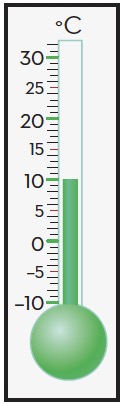
Quants graus ha pujat la temperatura des de l'hivern si llavors marcava −5 °C i ara marca 10 °C?
ℤ = {... −4, −3, −2, −1, 0, 1, 2, 3, 4...}
Els nombres enters poden ser tan grans o tan petits com vulguem; per tant, el nombre d'elements d'aquest conjunt és infinit.
3.1. La recta numèrica
Els nombres enters estan ordenats, i això permet que es puguin representar sobre una recta, que anomenem recta numèrica.
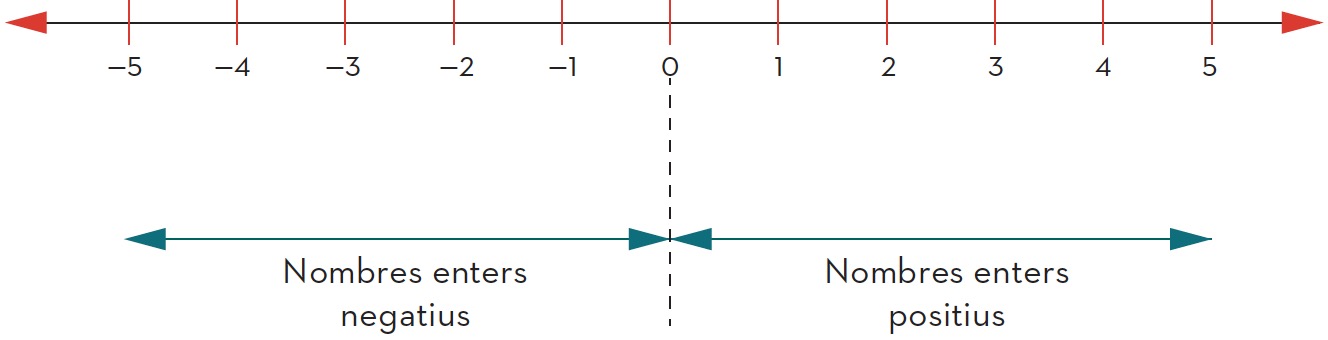
Cada nombre està situat a la mateixa distància de l'anterior i del posterior; és a dir, l'espai dibuixat entre cada parell de nombres és sempre igual.
La recta numèrica permet representar els nombres enters, calcular la distància entre uns i altres i veure les operacions.
La matemàtica Grace Chisholm Young va estudiar la representació dels nombres a la recta i la corresponent relació d'ordre.
Investiga en quins altres temes de matemàtiques va destacar.
Representa els nombres −4 i 5 a la recta numèrica i digues a quina distància estan l'un de l'altre.
- Representa els nombres a la recta numèrica.
- Compta els espais que hi ha entre l'un i l'altre.
Hi ha 9 espais, de manera que la distància que hi ha entre els dos és de 9 unitats.
3.2. Valor absolut
Acostumem a fer servir el valor absolut quan, per exemple, parlem d'altituds o profunditats en relació amb el nivell del mar, i també quan especifiquem dates d'abans o després de la nostra era.
Així, diem que la fossa de les Mariannes està, aproximadament, a 11 kilòmetres sota el nivell del mar; en canvi, no diem que està a −11 kilòmetres.
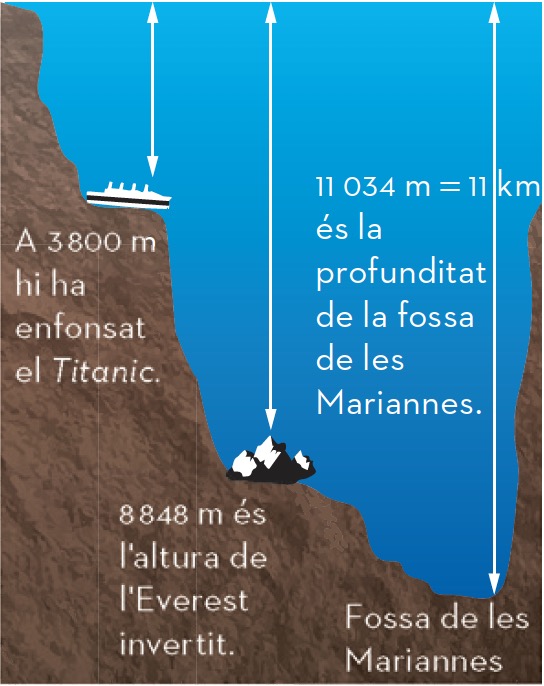
De la mateixa manera, diem que la civilització de l'antiga Grècia va començar 1200 anys abans de la nostra era; en canvi, no diem que va començar l'any −1200.
L'Helena vol anar d'excursió a la neu, però no té samarretes tèrmiques. Una seva amiga, la Marta, li deixa les 3 que té. D'aquesta manera, l'Helena ara té 3 samarretes, i la seva amiga, −3. Tot i que la situació és diferent per a l'una i l'altra, en realitat la quantitat intercanviada és la mateixa: 3 samarretes.
Com es pot expressar aquesta situació de manera matemàtica?
Si representem a la recta numèrica els nombres 3 i −3, veiem que la distància respecte al zero és igual en tots dos casos i que coincideix amb la quantitat intercanviada.
El valor absolut d'un nombre és la distància que hi ha entre aquest nombre i el zero.
- El valor absolut d'un nombre negatiu coincideix amb el valor numèric que s'obté si s'elimina el signe negatiu.
- El valor absolut d'un nombre positiu coincideix amb el valor numèric d'aquest nombre.
- El valor absolut de zero és zero.
- El valor absolut sempre és positiu o zero.
S'expressa de la manera següent:
|−3| = |3| = 3 |0| = 0
Representa els nombres el valor absolut dels quals és 4 i calcula la distància que hi ha entre l'un i l'altre.
- Compta 4 espais des del zero en les dues direccions.
- Marca els nombres finals amb punts i compta el total d'espais.
Els nombres de valor absolut 4 són 4 i −4, és a dir, |−4| = |4|= 4, i la distància que hi ha entre l'un i l'altre és de 8 unitats.
En els nombres positius, sempre és més gran el que té més valor absolut (està més a la dreta de la recta numèrica).
En els nombres negatius, en canvi, sempre és més gran el que té menys valor absolut (està més a la dreta de la recta numèrica).
Representa a la recta numèrica els nombres enters següents:
−13, −8, −2, 0, 1, 3 y 12
Calcula la distància que hi ha entre −2 i 3; 0 i 12; −13 i 0; −8 i 1.- Busca els nombres el valor absolut dels quals és 12 i calcula la distància que hi ha entre l'un i l'altre.
